三角形の外心,内 心,重心(4) ・三角形の外心,内心,重心の性質を 理解し,知識を身につけている。知 ・三角形の外心,内心,重心を作図す ることができる。技 観察 ワークシート 考え・基礎知識 三角形の外心,内心,各三角形の重心位置に点マーカ(+)を作図します(「 分割三角形の重心を作図しない」にチェックを入れている場合は除外)。色は分割線と同じ色になります。 多角形の重心位置に点マーカ( )を作図します。色は輪郭線と同じ色になります。三角形の内心を求めるにはどのよ 問題番号問いうに作図すればよいか。手順を説明 しなさい。 三角形の2角の二等分線をかく。 17 正解 その2本の二等分線の交点が三角 形の内心になる。 誤 答 例 つまずき原 因 分析と解消
Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
三角形 重心 作図
三角形 重心 作図-こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形の五心に関する面白い話題 $2$ 選 基本三角形の重心でも見た通り、三角形の重心とは、3つの中線の交点です。中線とは、頂点と、対辺の中点とを結んでできる線分のことです。 上の図で、 ap などが中線です。そして、 g がこの三角形 abc の重心です。 重心は、中線を $21$ に内分します。
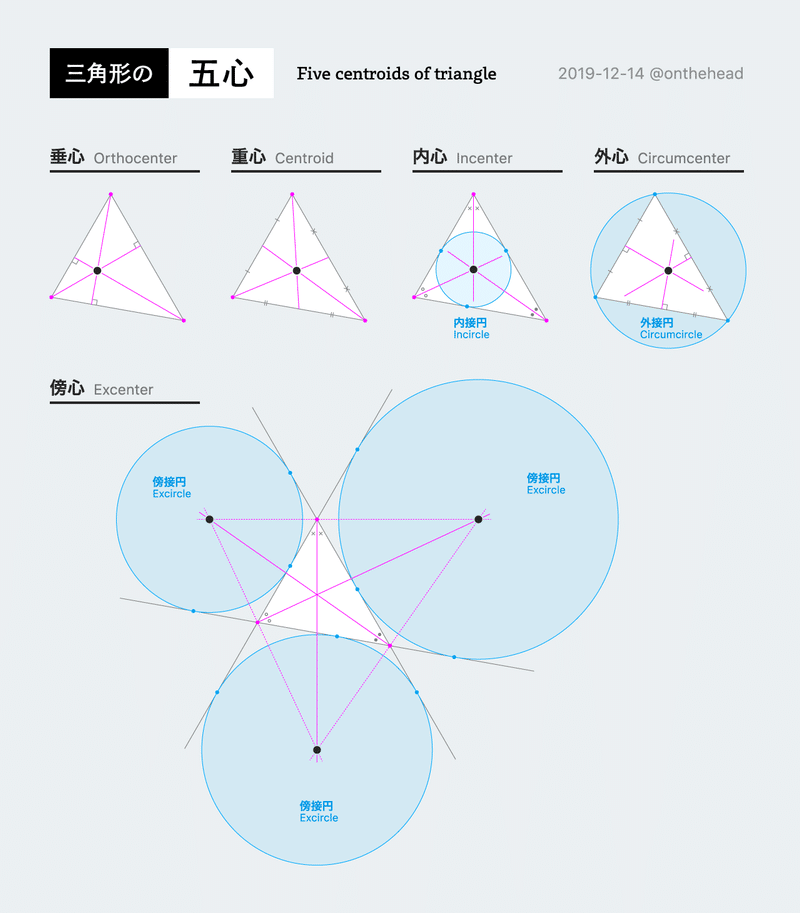



三角形の五心 宮澤聖二 Onthehead Note
T:三角形の心についてそれぞれの3本の垂線が一点で交わるかどうか作図して調べるんだ。 s:いちいち作図するなんて大変だよ。 t:GeoGebraを使えば大丈夫。 ⇒ 三角形の心 (2)「重心と外心の関係」と同じような関係の点を探すまた、対角線bdによって分けられる三角形の重心 g 3,g 4 を結ぶ線分上にも重心は存在するから g 1 g 2 との交点が四角形の重心である。 ところで、四角形の物理的重心は各辺の中点を結んでできる平行四辺形の交点であったが、同様に幾何的重心についても平行四辺形の交点として求めることが④三角形の高さを表す垂線を作図することができる。 ア、正答 53% イ、誤答 15% ウ、無回答 32% 学級の生徒の多くは、上記の通り数学を学ぶことについての大切さ(必要性)は感じている。
ここでは、三角形の重心の発展として、四角形の重心を考察する授業について提案する。 21 四角形の重心の作図 まず、図1のように四角形ABCDを⊿ABCと⊿ACDに分け、それぞれの三角形の重心G1,G2を作図すると、四角形の重心Gは線分G1G上に存2在する。三角形の重心は作図で求まりますから、厚紙に三角形と重心を作図して、三角形を切り出します。 当然ですが、 作図による誤差 もあります。 次に、三角形に小さな穴を開けて、ここに 黒い糸 を通して 重心は各頂点から引いた中線の交点なので、次のように作図できます。 STEP1 2 辺の垂直二等分線を引く
三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出《参考》 1)三角形の面積と重心 2)扇型の面積と重心 3)角錐台の体積と重心 r正三角形の場合は,内心・外心・重心・垂心が一致する。 イ. 外心は,三角形の3辺の中点を結んでできる三角形の垂心と一致する。 ウ. 三角形abcにおいて,角aの二等分線と外接円の交点を a' とする。同様にb',c' をとる。




三角形の五心 重心 内心 外心 垂心 傍心 高校数学なんちな




垂心とは 三角形の五心と位置ベクトルを解説 垂心の証明も 高校生向け受験応援メディア 受験のミカタ
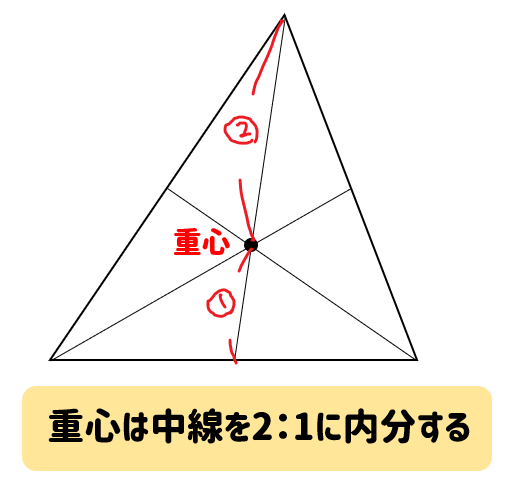
重心のおおよその位置を予想し,作図によって重心を見つけるという算数的活動を通して,図形の重心 に対する感覚を豊かにすることを目指した。本論文では,その授業実践の結果を報告する。 <キーワード>重心,正方形,長方形,l 字型図形,算数的活動 五心とは、三角形の 頂点や辺に関連する特徴的な つの点 のことです。 「重心」「内心」「外心」「垂心」「傍心」の つがあります。 名前に「心」とついている通り、それぞれあるものの中心になっています。 重心 重さの中心 ( 点で全体をバランス「三角形の3つの 線は1点で交わ り、その交点を 心という。 心は 線を : の比に 内分する。」 <実験>厚紙から切り取った三角形を 指で支えてみよう。 (重心を求めずに、まずは山勘で数回挑戦 させる。その後に、きちんと重心を求め



方程式が解けるようになる 中1数学の基本 29 三角形の四心 三角形には 4つの中心があります 内心 外心 重心 垂心 の4つです まずは 内心 内心は 三角形の3つの内角の二等分線の交点 3辺から等しい距離にある




傍心 私 数学の先生です
四角形から正三角形への等積変形について 中 込 雄 治1 黒 木 伸 明2 中学校までの学習内容を基にすれば、任意の四角形を三角形に等積変形したり、さらに三角形を長 方形や正方形に等積変形したりする三角形の重心とは? と聞かれたとき、上記の定義1を答えるのが一般的ですが、他にもいくつか答え方があります(全部同じ点を表しています)。 三角形の中線(3本あるが、どれでもよい)を 2 1 に内分する点(頂点までの距離が2、中点までの距離が1 最後に外心、内心、重心のポイントをまとめておきましょう。 外心 3辺の垂直二等分線が交わる点 各頂点から等しい距離にある 各頂点から線を結ぶと二等辺三角形ができるので、底角が等しい 円周角の定理が使える 内心 3つの角の二等分線が



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典
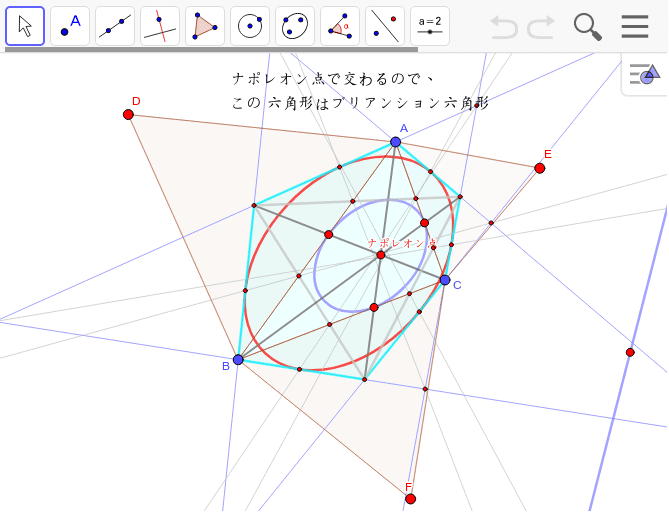



ナポレオン点と内接楕円 Geogebra
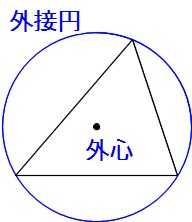
ここからは、 三角形の外心、内心、重心 について学習していこう。外心、内心、重心 は、簡単に言うと、 三角形の中心 のこと。 「三角形の中心」って、見方によって 色々な種類 があり、それぞれ別の点になるんだ。 まずは、 三角形の外心 がどんな点を表すかを解説していくよ。「三角形の重心」は,次のようにして見つけます。 ①適当な形,大きさで三角形 ABCをかきます。 ②3辺AB,BC,CAの中点(ちょうど真ん中の点)を見つけます。これは,それぞれの辺(線分)の垂直二等分線を作図すると,正確に見つけられます。三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。




三角形の五心 内心 外心 重心 垂心 傍心 の性質と証明を解説
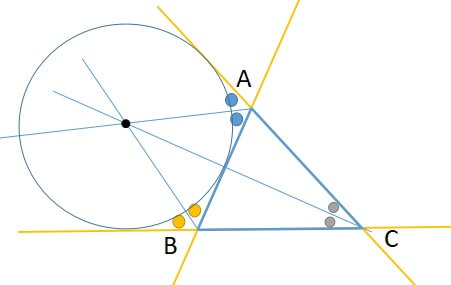



三角形の五心 内心 外心 重心 垂心 傍心 の性質と証明を解説
重心の作図 三角形の1つの頂点と、向かい合う辺の中点を結ぶ直線を中線といいます。 3本の中線の交点が、三角形の重心です。 頂点と辺の中点を結べばよいので、このときの作図は中点を見つける作図、つまり、垂直二等分線の作図です。 垂心の作図作図で重心を見つける方法の質問だと解釈し、説明します。 正五角形の対角線は下図の青線のようになり、これだけでは重心が見つかりません。 下図の対角線 と の交点を 、同様に、, , , を定めていきます。 すると、 と の交点が正五角形の重心となり三角形の重心を求める方法です。 標準の機能でやるには。 補助線を2本引いて求めることになります。 これを簡単にするには。 ToYoさんが、重心を求めwる外部変形を 公開されていました。 これを、ご紹介します。 外変 -面積図心bat をダブルクリック
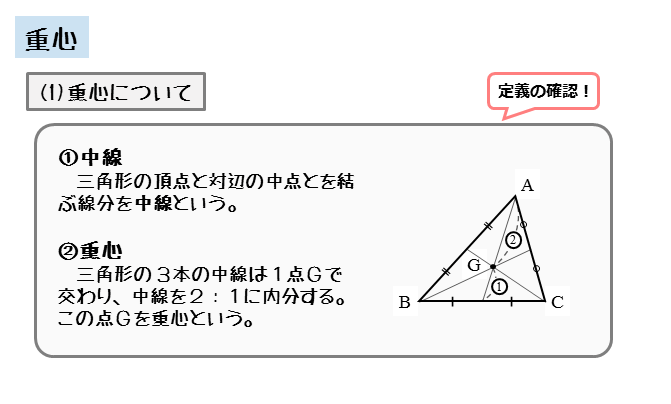



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
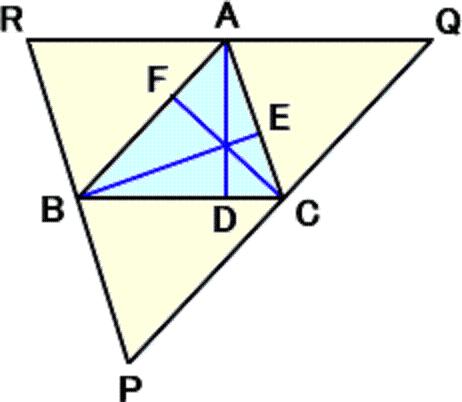
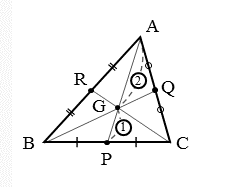
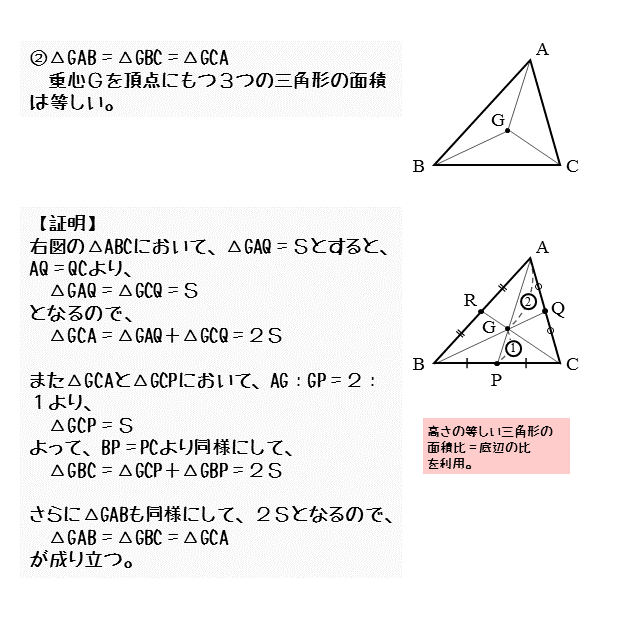
三角形ABCの外側に以下のふたつの正三角形を作図する。 一辺がABである正三角形ABD 一辺がBCである正三角形BCE この二つの正三角形の重心を作図しそれぞれをF,Gとする。 Fを中心として半径FA(=FB)の弧ABを書く。図形 作図 三角形 円弧 掛け ヘロン 正弦 余弦 正六角形 スパナ 「算数・数学」カテゴリーの人気ランキング 関数グラフ作成 GCalcPlus 式を入力するだけで、グラフを作成する数式グラフ化ソフト 二次元に加え、新しく三次元グラフにも対応 (ユーザー評価: 25 ) 重心について 三角形の頂点と対辺の中点とを結んだ線分 のことを 中線 と言います。 三角形では中線を3本引けますが、この 3本の中線は1点で交わります 。 この交わってできた点が 重心 です。 一般に、重心のことをアルファベットでGと表します。




高校数学a 三角形の重心1 基本 例題編 映像授業のtry It トライイット



垂心とは意味がある心か 数学のヒント
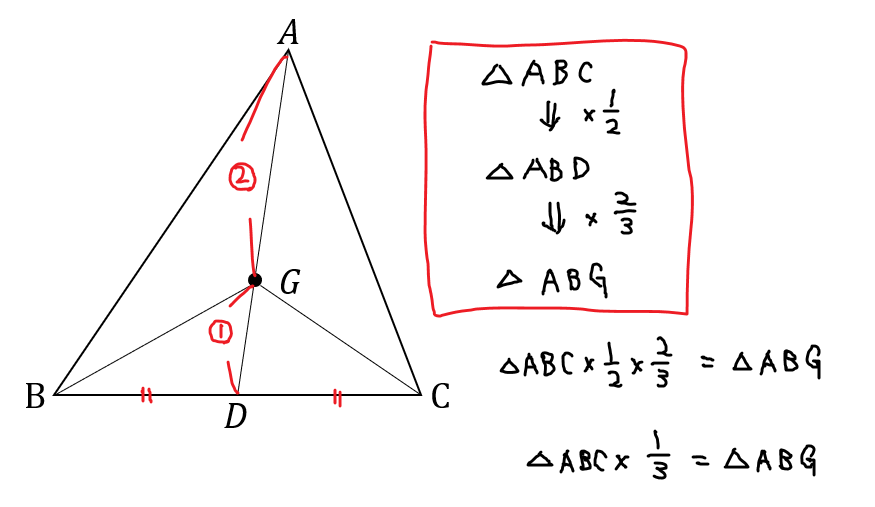
重心(g) 垂心(h) 外心(o) 内心(i) 傍心(i a, i b, i c) 三角形の1つの内角の2等分線と他の2つの角の外角の2等分線の交点。 正三角形の四心(内心,外心,垂心,重心)は一致し, 内心,外心,垂心,重心のうち2つが一致すれば正三角形となる。任意の点Gを重心とする三角形の作図 (1) Gの外側に線分を引く (2) 中点をとる (3) MとGを結ぶ (4) MG:GC=1:2になる点をとる (5) Gを重心とする△ABCができる四角形の重心と面積比 back 2直線の交点 四角形の重心を作図するのに、2通りの三角形の分割をせず、1通りの分割した三角形の重心 と面積比から作図できることをベクトルを用いて証明し、実際に作図することで、ベクトルに




三角形の内接円の作図法と証明について 三角形の内接円の作図法と証明 数学 教えて Goo



外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ




Neaaxnyw34gfgm




三角形の垂心とは 垂心の性質と証明




図形の性質 重心について 日々是鍛錬 ひびこれたんれん




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学



物体の重心
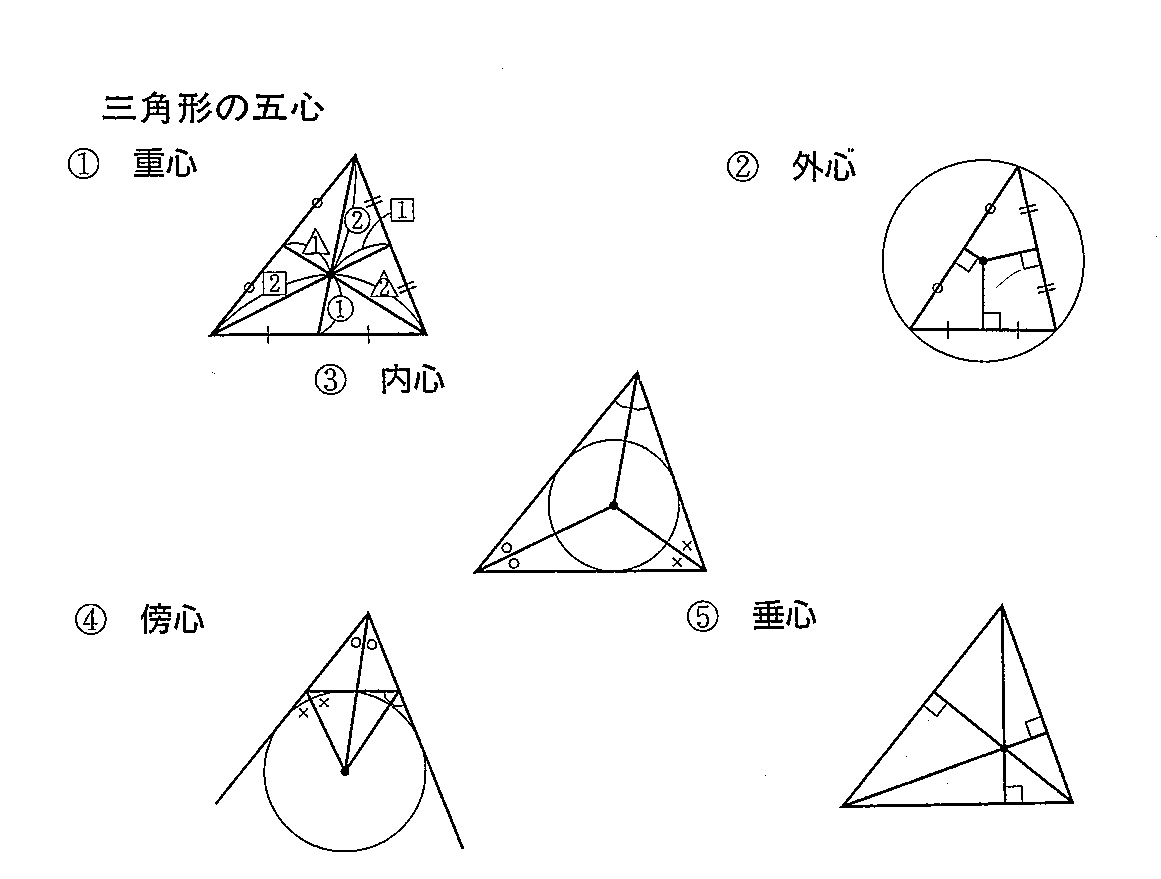



五つの心 倉予備へ行こう
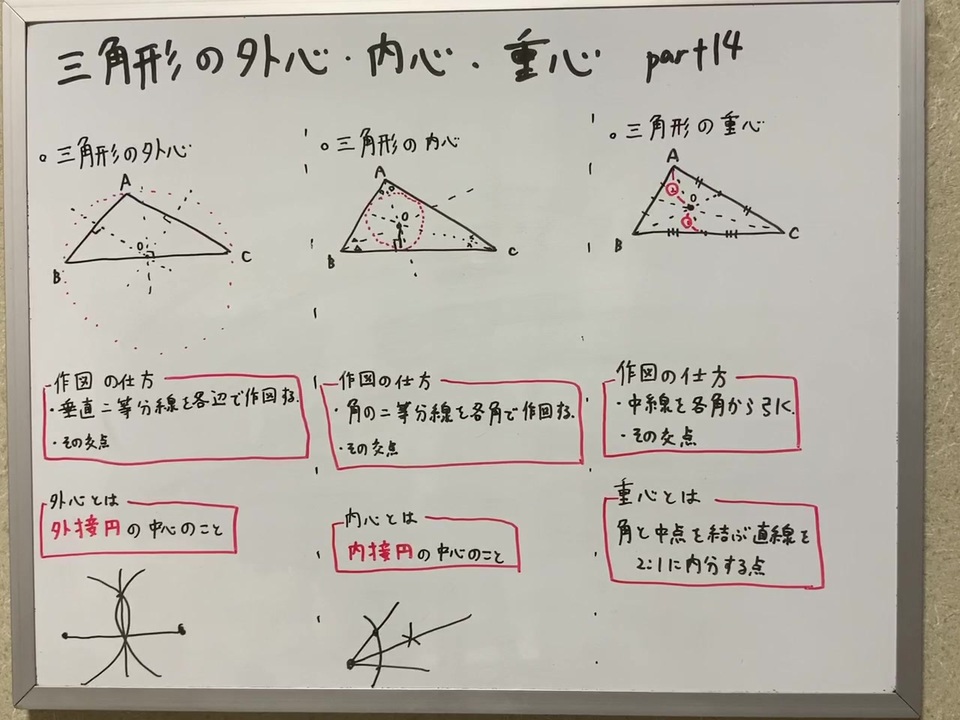



数学a14三角形の外心 内心 重心 三角形にある有名な三つの中心 よく出てくるので覚えておきましょう ニコニコ動画




2 三角形の外心の作図 Youtube




図形の性質 重心について 日々是鍛錬 ひびこれたんれん




三角形の重心の性質と証明 座標とベクトルの求め方も徹底解説
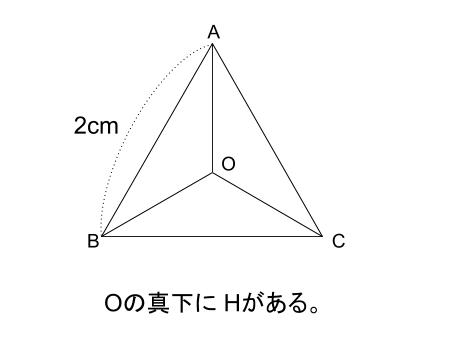



正四面体の体積と三角形の重心 中学数学の無料オンライン学習サイトchu Su
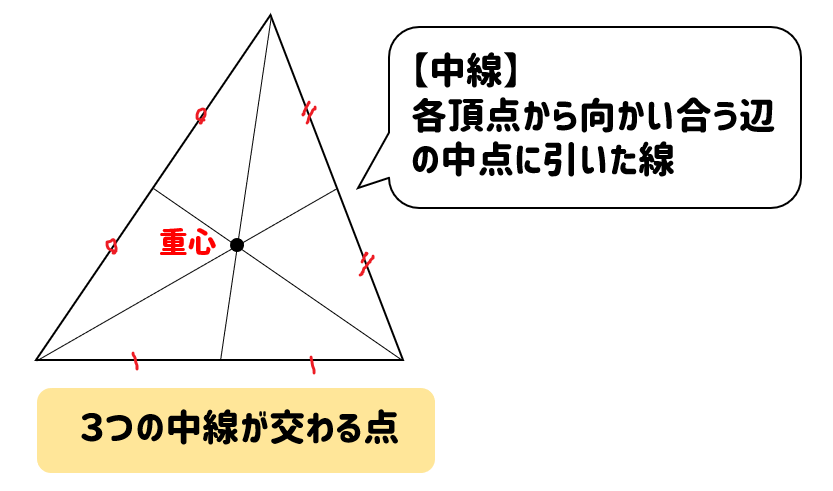



外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ
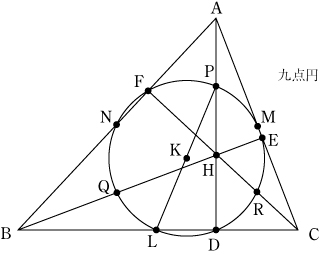



授業実践記録



Studydoctor三角形の内心 高校数学a Studydoctor




シュリヤントラ Sri Yantra の作図 Canada S Windview



外接円 外心について
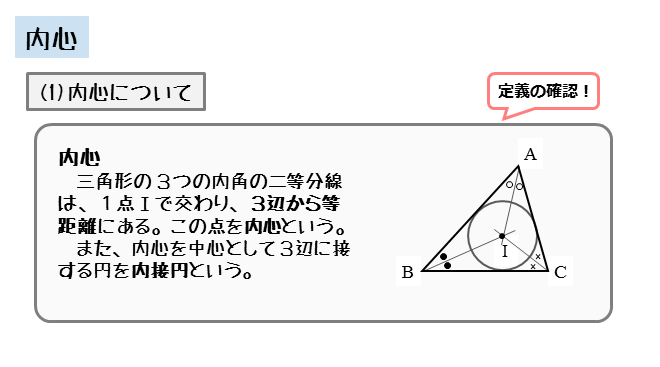



図形の性質 内心について 日々是鍛錬 ひびこれたんれん
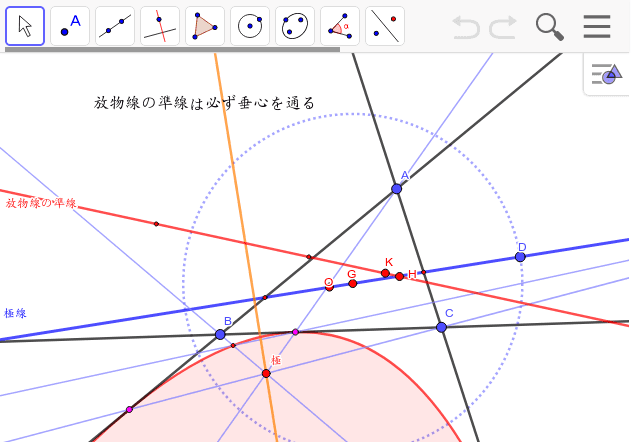



極線が重心を通る放物線の準線は垂心を通る Geogebra



重心を理解する フィジオ八王子



2 四角形の重心
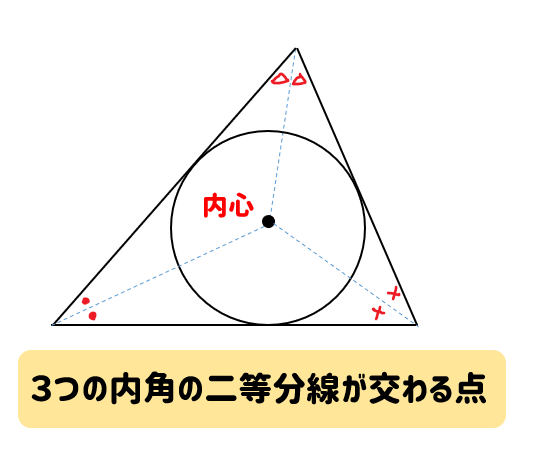



外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ




Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



垂心について




垂心とは 三角形の五心と位置ベクトルを解説 垂心の証明も 高校生向け受験応援メディア 受験のミカタ




イラスト豆知識 三角形の性質 株式会社オプライン



台形の重心は 1分でわかる意味 重心位置の求め方 面積




三角形の重心について知っておきたい知識まとめ 理系ラボ
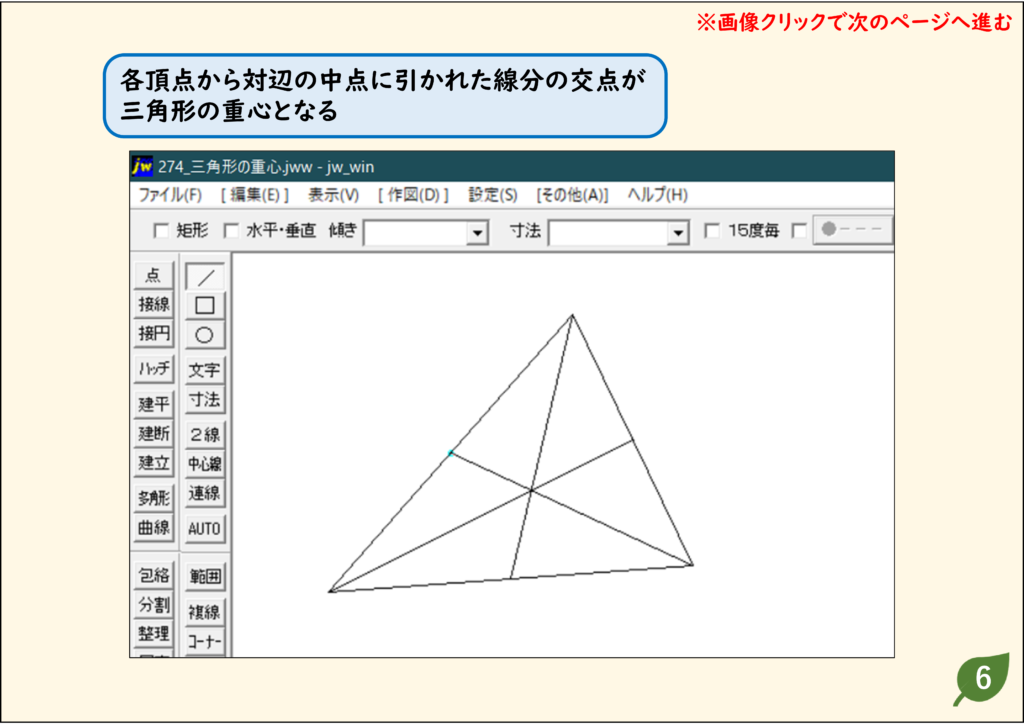



簡単 Jwcad 274 線 三角形の重心を求めるには 使い方 Jw Cadの使い方




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学




勉強しよう数学 三角形の垂心の図の全ての線分を三角関数の積で表す



作図円に内接する正三角形 中心の分からない円の円周上の指定の点を頂点の Yahoo 知恵袋



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




作図 三角形の高さをコンパスを使ってかく問題を解説 Youtube



外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ
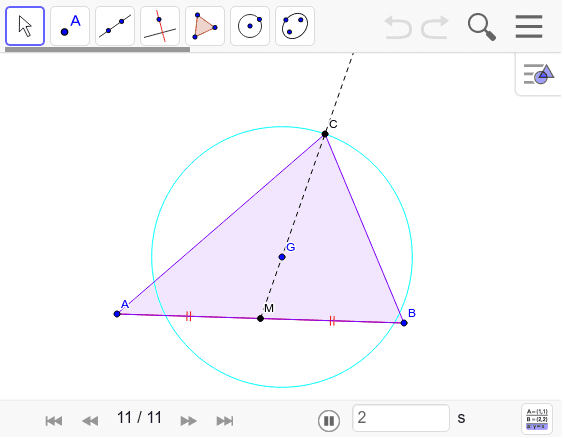



任意の点gを重心とする三角形の作図 Geogebra




4 三角形の内心 Youtube



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
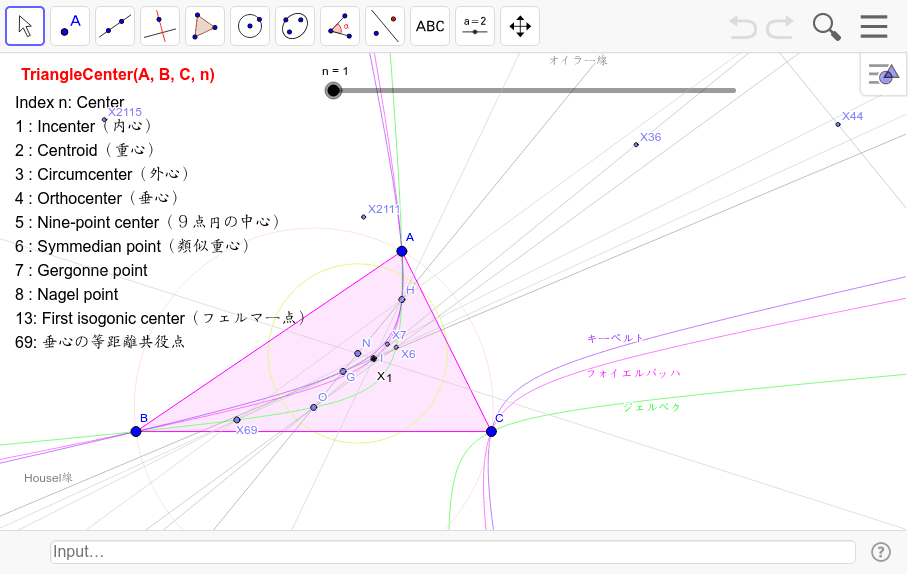



三角形の心の作図のコマンド Geogebra



コンパスで内心外心重心を作図しろという問題が出たとした時にどのように書けばいい Yahoo 知恵袋
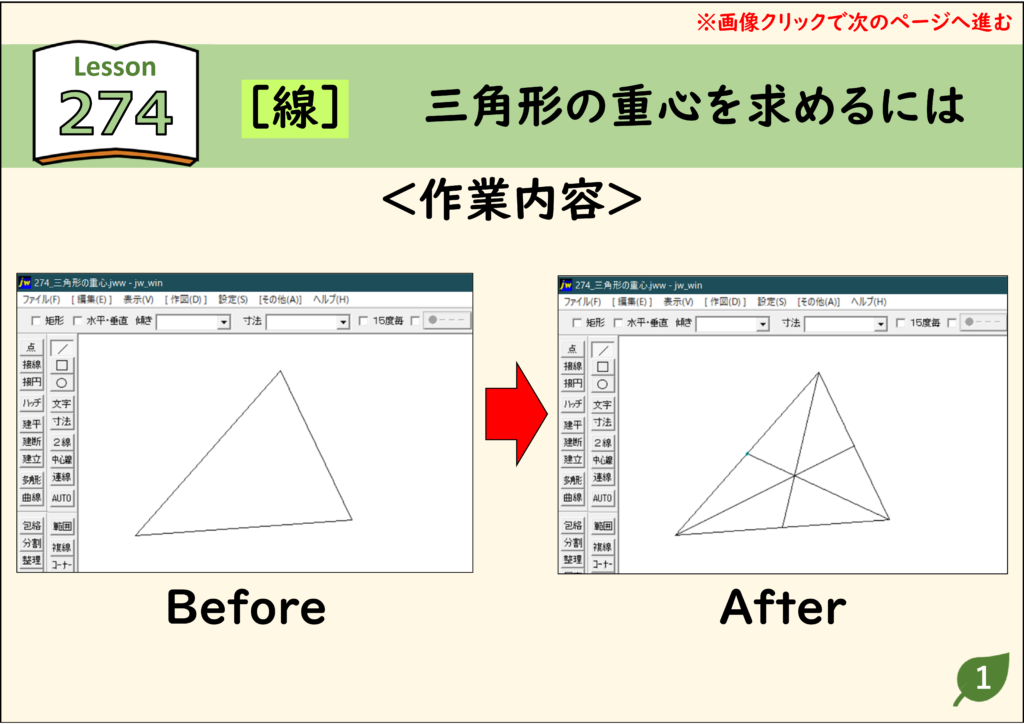



簡単 Jwcad 274 線 三角形の重心を求めるには 使い方 Jw Cadの使い方




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学




高校数学a 三角形の内心2 実践 例題編 映像授業のtry It トライイット



垂心について




高校数学a 三角形の内心1 基本 映像授業のtry It トライイット



重心を理解する フィジオ八王子




垂心とは 三角形の五心と位置ベクトルを解説 垂心の証明も 高校生向け受験応援メディア 受験のミカタ




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学



任意に与えられた図形の重心を作図する方法はありますか 直線で囲まれ Yahoo 知恵袋



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



正五角形の重心はどのようにして見つけますか Quora



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



作図の例題解説 作図 中学数学の計算機図形エディタで4種類の図形データの作成ができます 1 静止図形のデータ作成 2 作図シミュレーションのデータ作成 3 図形のシミュレーションのデータ作成 4 図形シミュレーターのデータ



Pointline Dynamic Geometry Software Without Construction Procedure



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




Euclidea 3 2 角と垂心を通る三角形の作図 解説 みのまわりのものたち




重心の位置 理科好き子供の広場




高校数学a 三角形の重心1 基本 映像授業のtry It トライイット



3 多角形の重心



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




三角形の五心 宮澤聖二 Onthehead Note



2 四角形の重心



内接円 内心



重心を理解する フィジオ八王子



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




三角形の外接円と外心 内接円と内心 中学 高校数学 身勝手な主張



1 2 三角形の外心の作図 2
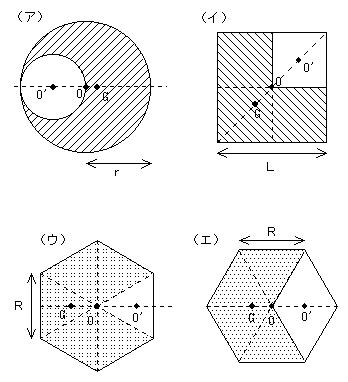



剛体の重心
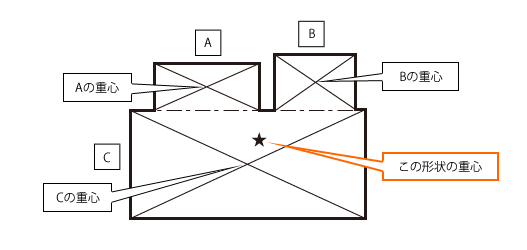



重心について 機械工学と自動機設計 8 技術情報 Misumi Vona ミスミ



Geogebra遊び




No 2さんへ台形の重心の求め方について 34チャンの兵庫de日記 W 34チャンのブログ Lifestyle




垂心とは 三角形の五心と位置ベクトルを解説 垂心の証明も 高校生向け受験応援メディア 受験のミカタ




三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア




中1 重心 垂心の作図 中学生 数学のノート Clear




四角形の重心の求め方の定義名 図のような四角形の重心の求め方には定 数学 教えて Goo




三角形の重心の性質と証明 座標とベクトルの求め方も徹底解説



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ




図形の性質 重心について 日々是鍛錬 ひびこれたんれん



五心 重心 内心 外心 垂心 傍心 とは 求め方や性質 受験辞典
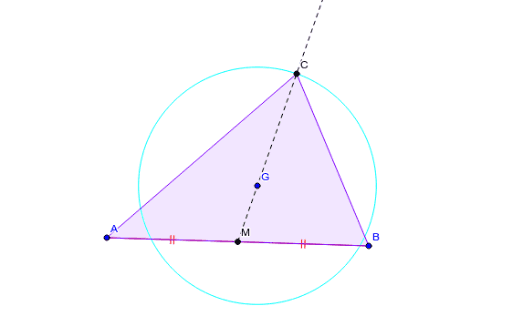



任意の点gを重心とする三角形の作図 Geogebra



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典




形態の基礎理論 三角形の重心



方程式が解けるようになる 中1数学の基本 29 三角形の四心 三角形には 4つの中心があります 内心 外心 重心 垂心 の4つです まずは 内心 内心は 三角形の3つの内角の二等分線の交点 3辺から等しい距離にある



三角形の重心の性質と証明 座標とベクトルの求め方も徹底解説



0 件のコメント:
コメントを投稿